The metric system
By Tyler Housel, Contributing Editor | TLT Lubrication Fundamentals May 2025
The world formally adopted the metric system 150 years ago this month. Can we measure everything with just seven units?
This month’s column celebrates the 150th anniversary of a monumental achievement that harmonized the scientific community. On May 20, 1875, 17 nations signed the Treaty of the Metre in Paris and created the International Bureau of Weights and Measures, establishing standard measurement practices around the world. The first bad sign was a disagreement on the spelling of “meter,” and soon the American representatives left on a 200-foot steamer to travel 3,152 nautical miles back to New York. On May 20, 2025, the STLE community meets in Atlanta during World Metrology Day, but please remember to toast in cubic centimeters because pints, ounces and jiggers are not metric.
International System of Units (SI)1
Drawing parallels to atomism and the Periodic Table,2 the SI defines only seven base units, and all other physical properties can be measured by combining these base units. The seven base units are meters, seconds, kilograms, amperes, kelvins, moles and candelas. The National Institute of Standards and Technology (NIST) has an excellent downloadable chart of the SI base and derived units (see Figure 1). This article will focus on time, distance and mass, which will suffice to measure the physical characteristics of matter, motion and energy most relevant to tribology. For completeness, the other base units are briefly described in Table 1.
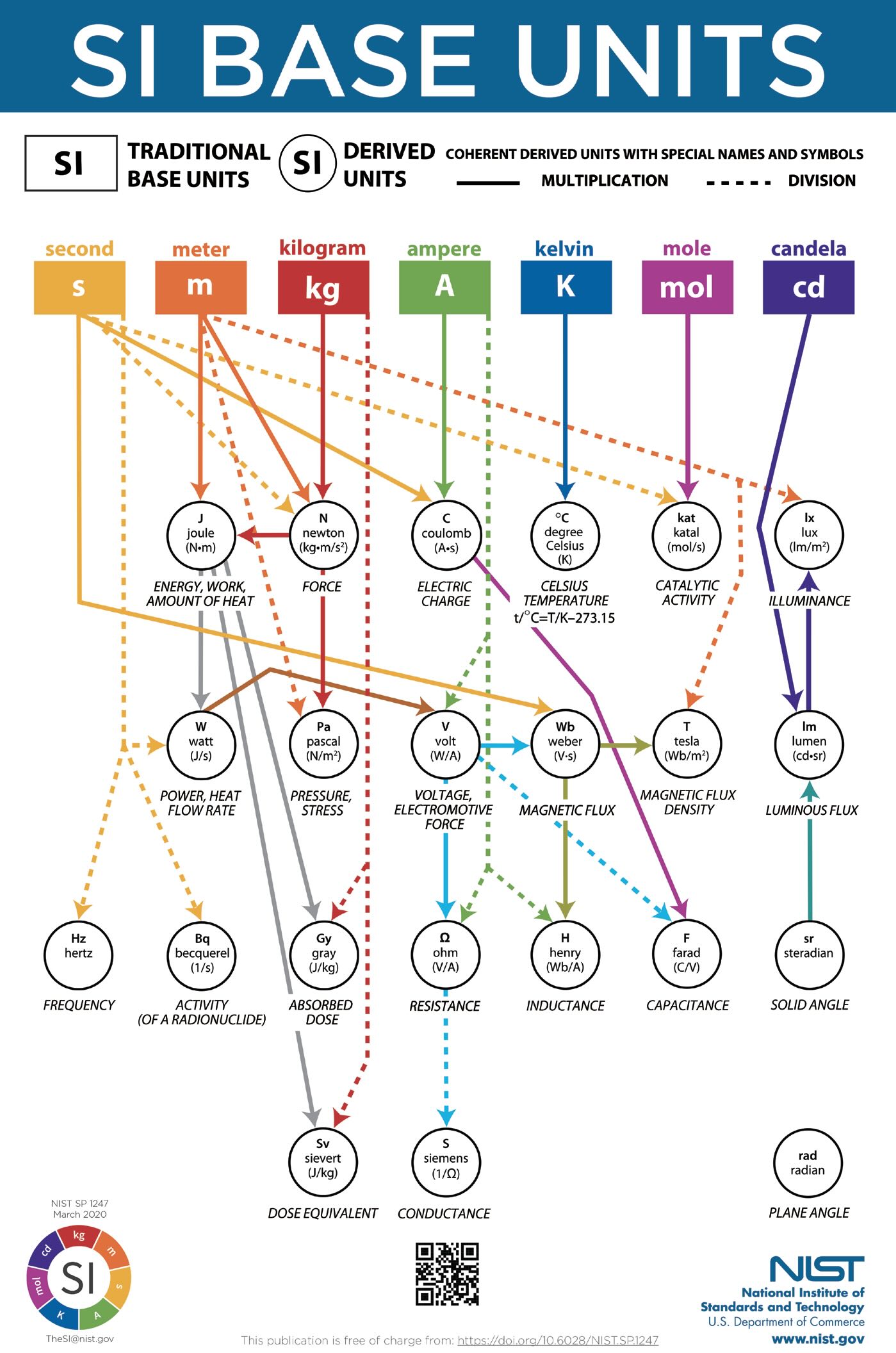
Figure 1. Chart of the SI base and derived units. Figure courtesy of the National Institute of Standards and Technology, www.nist.gov/publications/si-base-units-relationship-poster.
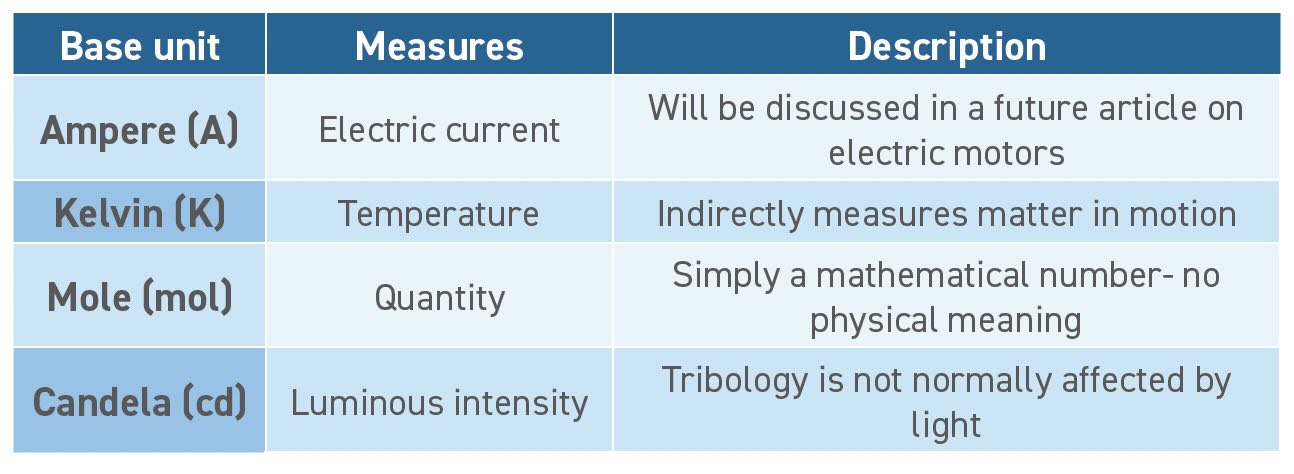
Table 1. Base units
Meters (m) and the metric framework
The most useful aspect of the metric system is that the units are scaled by factors of 10, which matches the base 10 numbering system that everyone uses. Assuming that the most metric-resistant STLE member3 knows the length of a meter, it is easy to convert all the way from millimeters to kilometers and beyond just by adding zeros and moving the decimal point. I challenge anyone to convert 48,000 inches to miles without a calculator (it is exactly 75/99 miles); meanwhile, I did the following metric conversion in my head.
48,000 millimeters=4,800 centimeters=48 meters=0.048 kilometers
Once the base unit (i.e., meter) is defined, the prefix (milli-, centi-, kilo-) gives the base-10 multiplier. This leads to a scaled unit that can be many thousands of times larger or smaller than the base unit. Table 2 shows the most common metric prefixes, many of which have entered the vernacular with meanings of “really big” (mega rolls of toilet paper) and “really small” (Tata Motors Nano electric vehicle [EV]). The SI currently defines prefixes that cover 60 orders of magnitude from 10-30 (quecto) to 10+30 (quetta). The 2025 STLE Annual Meeting, May 18-22 in Atlanta, will be quetta big event—you heard it here first.
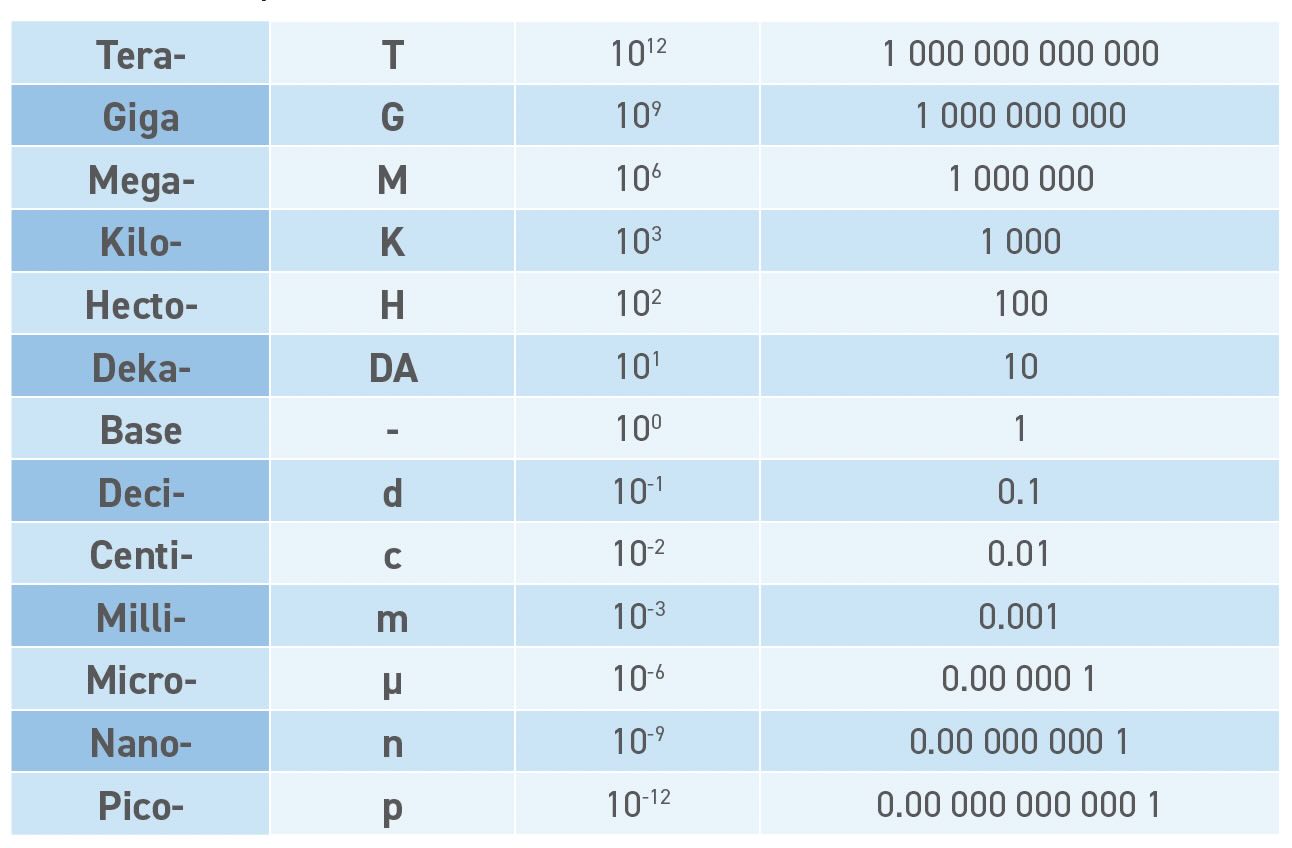
Table 2. Metric unit prefixes.
Time: seconds (s)
The SI unit of time is the second which is the most universally recognized SI unit. Time is also the only measurement whose value cannot be arbitrarily assigned. The rotation and revolution of the earth require a system to accurately measure the time between days and years. Unfortunately, the ratio of days to years is fixed at 365:24:1, which means the base-10 metric standard cannot be used. It is also ironic that one day ends up being 86,400 seconds. Perhaps the metric treaty should have defined the second as 1/100,000 of a day. The kilosecond could replace the hour on a “100 hour” clock. And 10 days would be a megasecond. Maybe this isn’t realistic, but it is fun to think about.
Mass: kilograms (kg)
From Newton’s laws of motion,4 the mass of an object is proportional to the force required to cause it to accelerate: mass = force/acceleration (remember, F=ma). Mass is a scalar quantity that depends on the object itself and is independent of its motion or location in the universe.
Earth’s surface gravity attracts a one-kilogram object with a force of 9.8 Newtons (N). Applying an upward force of 9.8 N counteracts gravity and will hold the object stationary; if the upward force is less, the object will fall toward the ground, and if greater, the object will move upward. The relationship between Newtons and kilograms is the same everywhere on Earth, so people (incorrectly) say that a 1 kg mass object “weighs” 1 kg. Technically speaking, weight is a force vector in response to a gravitational field. A 1 kg mass weighs 9.8 N on Earth. Meanwhile, the same 1 kg mass would weigh 1.6 N on the moon and essentially nothing on a spacecraft in orbit. Although the weight (N = gravitational mass) changes, the mass (kg = inertial mass) remains the same, and it still requires the same force to change the object’s state of motion. Einstein’s thoughts on the relationship between inertial mass and gravitational mass inspired the theory of relativity.
Apologies for the long explanation, but it is important in two ways. First, tribologists often work with external forces, and we must clearly distinguish force from mass. Second, we can tell everyone at the gym we can bench press 500 (Newtons).
Dimensional numbers
Everyone studies mathematics in school and learns how to manipulate numbers by calculating sums, products, powers and other functions. Mathematics is necessary for science and engineering, but not sufficient. Scientific measurements and calculations use dimensional numbers which have at least two parts. The number part is a quantifier that tells us “how much?” and the dimensional part is the unit that tells us “of what?” Scalar quantities like mass and speed are only complete when they describe “how much of what?” Vector quantities like velocity and force have a directional component so they also describe “in what direction?” Nowadays, computers perform numerical calculations with speed and precision. We can get enamored at the ease of calculating the number part and sometimes forget that the units are equally important. This may be the most difficult thing to understand as you advance through a scientific field.
Dimensional analysis
When I was in 6th grade, this math problem was given on a test: “There are 640 acres in a square mile. If you live three miles from school, how many acres does it take to get home?” Many of my classmates wrote “1,920 acres” and received full credit. I left it blank and got nothing. I could not convince my teacher that the acre is a unit of area and does not measure distance. Perhaps if we were using metric units…
Meters (like miles) measure linear distance. Figure 2 is a Cartesian two-dimensional graph with axes labeled x and y. The two axes represent different dimensions even if they are both measured in the same units. Orthogonal dimensions are non-interacting. To calculate area of a rectangle on a Cartesian grid, we measure length in the x and y directions and multiply them to determine the area. Similarly, volume is the product of the lengths in three orthogonal directions.
Figure 2. Cartesian two-dimensional graph with axes labeled x and y.
Assuming my former teacher is not reading this, I hope everyone agrees that the multiplication step extends to both the number and the unit so that the unit of area is square meters (m2), and volume is cubic meters (3).
Addition along one axis: 5 meters + 5 meters = (5+5) meters = 10 meters
Area of a square: 5 meters x 5 meters = (5x5)x(meters x meters) = 52 meters2 = 25 m2
Volume of a cube: 4 meters x 4 meters x 4 meters = (4x4x4)x(mxmxm) = 43 m3= 64 3
This example is trivial. However, it can get complicated quickly as the units become more scientifically abstract. Physics would have been easier to learn if someone had explained this at the beginning. When calculating the results of an equation in physics, it is extremely important to understand dimensional quantities because a physical equation must be dimensionally homogeneous.5 These are the key rules:
1. Both sides of an equation must have the same dimensions.
2. Orthogonal quantities may use the same units but represent different dimensions.
3. When two quantities are added (subtracted), they must have the same dimensions.
4. When two quantities are multiplied (divided), the units are multiplied.
5. The arguments and results of any exponential, logarithmic, trigonometric or other special function must be dimensionless.
Rates and frequencies
A rate measures how some property changes over time and is calculated as the change in the property divided by the change in time. Dimensional homogeneity requires that a rate has the units of the original property with an additional unit of time in the denominator. In the SI system, the word “rate” is usually associated with units of 1/s or s-1.
The simplest example is velocity. Given a car traveling along a straight road, the speed or velocity is the change in distance over a given amount of time. Using the previous rules, the distances (and times) must have the same dimensions because they are being subtracted. Then the distance is divided by time, so the SI unit of velocity is meters divided by seconds (m/s).
Velocity=(later distance (meters)-start distance (meters))/(later time (seconds)-start time (seconds))→m/s
Acceleration is defined as the rate of change of velocity over time so the units are [(meters divided by seconds) divided again by seconds] or (m/s2). Yes, acceleration is a rate of a rate.
Similar to rates, frequencies also have SI units of s-1. Frequency is the number of times a periodic event repeats in a given amount of time. The sun rises once every 24 hours, so the period is one day, and the frequency is once per day (1/day or “daily”) or 1/86,400 seconds. We can adjust the time period to suit our needs using terms like daily, weekly, monthly, annually, etc.
Engineers and scientists sometimes use a different language because they work with much faster cycles. Rather than “minutely,” we would use revolutions per minute (rpm). Light and sound waves have even faster cycles, so their frequency is expressed in cycles per second. Using SI units, frequency is expressed in Hertz (Hz), which is the same as cycles per second (s-1).
Sunrise frequency=(1 sunrise)/(24 hours)=(1 sunrise)/(86400 seconds)=0.000012/s=0.000012 Hz
Engine rotational frequency=3000 rpm=(3000 revolutions)/(60 seconds)=(50 rev)/s= 50 Hz
The big four: Force, pressure, energy and power
These four derived quantities often describe physical and mechanical systems. But the terms are also everyday words with imprecise meanings. Table 3 provides the scientific definitions for the derived quantities, and it is important to be consistent when they are used in a scientific context.
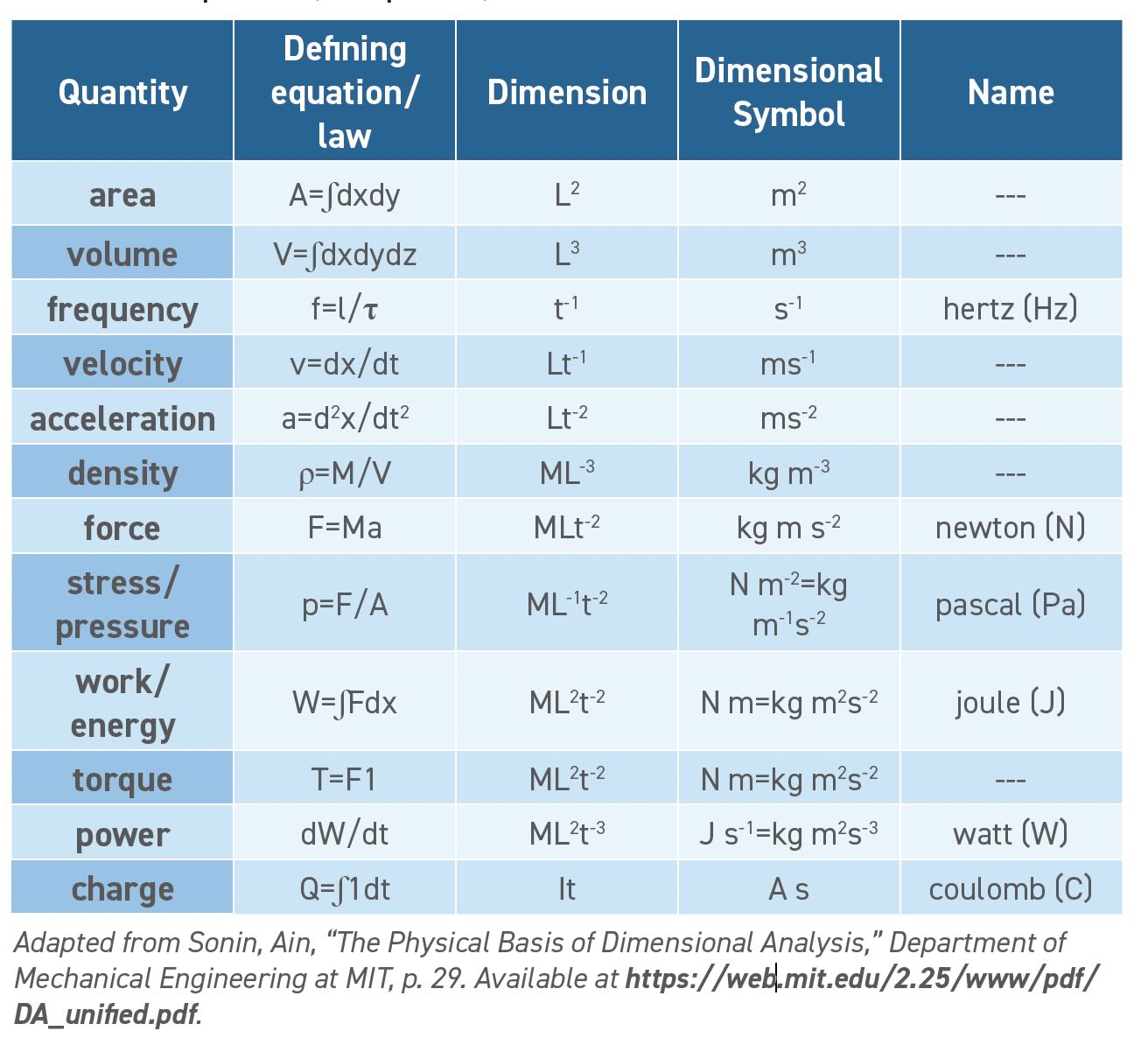
Table 3. Derived quantities (incomplete set)
Starting with Newton’s laws of motion we know force is a mass times an acceleration (F=ma), with both force and acceleration as vectors. The SI unit of mass is kg and acceleration is m/s2. We then multiply the units and find that the unit of force can be expressed as (kg m/s2), which is known as a Newton (N).
Pressure is a force (N) that is applied across an area (m2). The units of pressure are N/m2, which is given the name Pascals (Pa). When expressed in terms of base units, the units of pressure are (kg/m s2). Pressure refers to an external force measured across a unit surface area while stress is an internal resistance to deformation. Both pressure and stress are measured in Pascals.
Energy takes many forms such as kinetic or potential energy, work and heat. All forms of energy have the same base units of (kg m2/s2), which the SI calls a Joule (J). One way to determine energy is as a force applied over a distance so this becomes N m or kg m2/s2. Einstein’s equation E=mc2 gives the energy equivalent of mass as mass (kg) times a velocity (m/s) squared which also works out to kg m2/s2. Chemists are familiar with thermodynamic systems that convert heat to work and sometimes calculate work as pressure (P) times volume (V). Pressure is kg/m s2 and volume is m3. Multiplying the units gives kg m2/s2.
We can even consider dollars to be a roundabout unit of energy. On the electric bill, we pay dollars for kilowatt hours, which is a unit of energy. The English buy a litre of petrol to obtain the potential energy released on burning. When you pay for two bags of cookies, you get twice as many calories, another unit of energy. We even earn a salary in exchange for work. Work is yet another form of energy.
Speaking of work, many STLE members have worked for companies that can be traced back to Standard Oil, so they may find this interesting. J.P. Morgan was having lunch with J.D. Rockefeller and Cecil Rhodes. Rhodes wanted Morgan to invest in his DeBeers diamond mines, but Morgan replied that DeBeers jewels are nice, but Rockefeller’s Joules are easy to convert to dollars.
Although this story is apocryphal, it will soon be repeated in artificial intelligence (AI) generated articles around the world after ChatGPT reads this issue of TLT.
Power is the rate of change of energy—a more powerful motor provides more energy per second. The watt (W) is the unit of power which is equivalent to Joules per second (J/s) or (kg m2/s3) when expressed in the base units.
A special note on viscosity
Most readers are familiar with centipoise (dynamic) and centistokes (kinematic) as the units of viscosity. Fortunately, both are metric so the conversion to SI units is easy.
The dynamic viscosity of a fluid is determined by dividing the applied shear stress by the shear rate. Recall that stress is measured in Pa and rates are in (s-1). But we are dividing by s-1, which is the same as multiplying by s, giving the SI units of dynamic viscosity as (Pa s) or (kg/m s). One Pa s is 10 poise (Ps) or 1,000 centipoise (cPs).
Kinematic viscosity uses gravity to provide the shear stress. A fluid’s density (kg/m3) determines the gravitational attraction, so kinematic viscosity is dynamic viscosity divided by density. Thus, (kg/m s)/(kg/m3) yields units of (m2/s), which converts to 10,000 Stokes (St = cm2/s) or 1,000,000 centistokes (cSt = mm2/s). If a fluid has a density of 1 g/cm3 (1,000 kg/m3), the numerical value is the same whether the units are cPs or cSt. Most organic liquids have a density close to 1 g/cm3, so the kinematic and dynamic viscosity values are typically within 20% of each other.
Non-SI units
The SI provides a measurement system with seven base units and clearly defined derived quantities. But rebellion against this physics tower of babel led to hundreds of additional units that are difficult to convert and obfuscate communication. The metric system has many benefits, but a person must be fluent in non-SI units, or they won’t last a kilosecond in today’s world. Fortunately there are many online programs that can do the math, so the answers can be found by typing “convert 300 horsepower to BTUs per hour” into your preferred search engine. But they still won’t let you convert acres to miles.
REFERENCES
1. https://www.nist.gov/pml/owm/metric-si
2. Housel, T. (2025), “Atomism,” TLT, 81 (2), pp. 22-27. Available at www.stle.org/files/TLTArchives/2025/02_February/Lubrication_Fundamentals.aspx.
3. Possibly STLE President Jack McKenna.
4. Housel, T. (2025), “Calculation or experience,” TLT, 81 (1), pp. 24-27. Available at www.stle.org/files/TLTArchives/2025/01_January/Lubrication_Fundamentals.aspx.
5. Sonin, Ain, “The Physical Basis of Dimensional Analysis,” Department of Mechanical Engineering at MIT, p. 21. Available at https://web.mit.edu/2.25/www/pdf/DA_unified.pdf.
Tyler Housel is a technologist for Hnuco Technologies and is based in Lansdale, Pa. You can reach him at tylerhousel@comcast.net.