Calculation or experience
By Tyler Housel, Contributing Editor | TLT Lubrication Fundamentals January 2025
How do you best approach lubrication and tribology?

I am honored that STLE asked me to follow Dan Holdmeyer as the author of TLT’s Lubrication Fundamentals article in 2025. This feature has always been a must-read part of TLT with a long history of excellent writers. I look forward to exploring some of the fundamental concepts of lubrication and hope to maintain the high quality the readers have come to expect.
Tribology is a science that seeks to understand the interaction between two or more solid bodies that are in relative motion and close enough contact to allow a direct transfer of mechanical forces between them. It took a long time to discover the laws of motion and force that govern gears, bearings and other machine elements. Table 1 presents a timeline to introduce some key players who made significant contributions along the way.
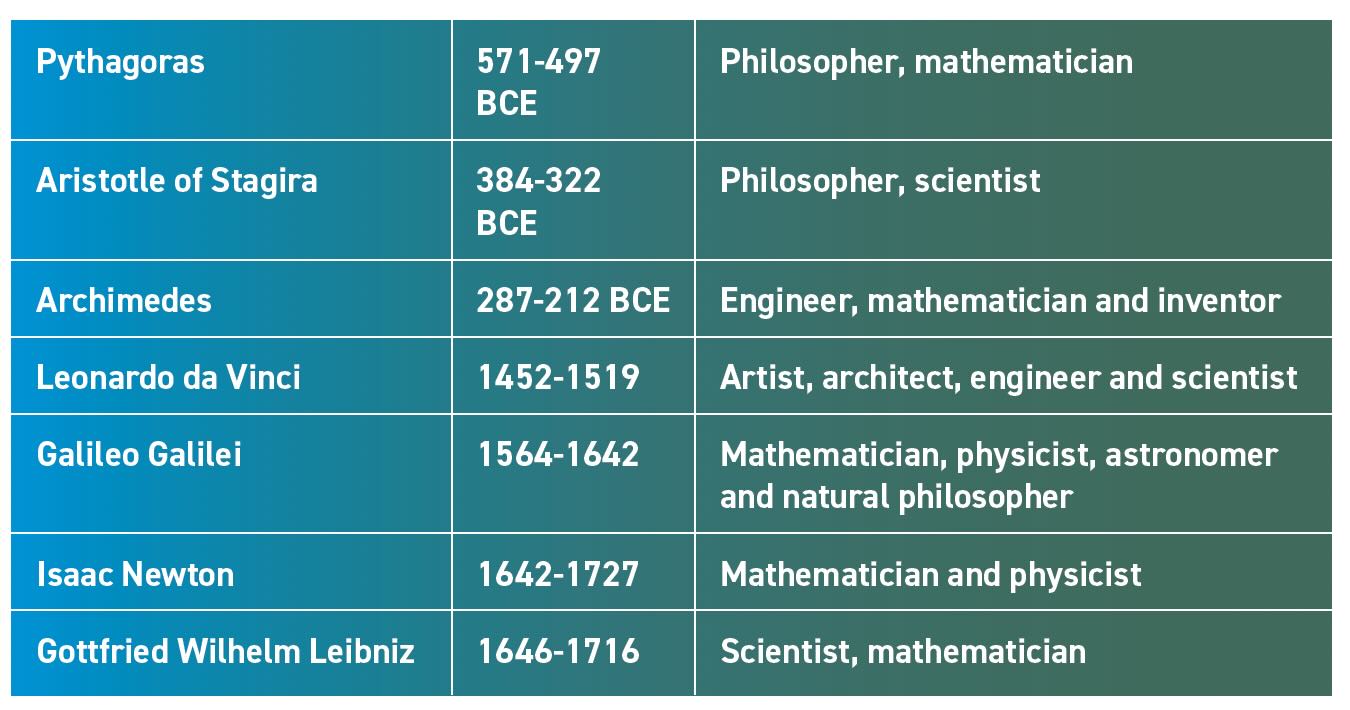 Table 1. Notable players developing the concepts of force and motion6
Table 1. Notable players developing the concepts of force and motion6
The laws of physics and the tools of engineering can now be used to calculate an analytical solution to almost any tribological problem. With time, STLE members also develop a keen sense of observation and a network of experienced professionals that may guide us to the same conclusion without the mathematical steps required for an analytical solution. So, is it best to approach tribology through calculation or experience?
Lubricants were first developed in ancient times through observation and trial and error. Ancient civilizations constructed settlements, pyramids and chariots using wheels, rollers, levers, sleds and pulleys to expand the abilities of the human body. And they recognized that lubricious substances would allow them to move heavy objects with less effort. This know-how was gained through experience.
Pythagoras argued that experience alone could not reveal truths in the world. Philosophers could debate the meanings of life, love and lubrication—but they could not be certain that new evidence might invalidate their conclusions. Instead, Pythagoras believed that only mathematics revealed ultimate truths which, once proven, could not be challenged. Number math was already well established as an accounting tool, and everyone agreed two plus two always gives four. Mathematical proofs led to absolute truths, so he believed that reality did not exist in nature, but rather reality was the mathematical framework that shows the underlying structure of the imperfect natural world. Physical objects could be modeled by idealized geometrical structures to predict their behavior. Pythagorean geometry was essential to enable early builders a way to calculate how to distribute loads and manage weight more efficiently. But it only provided a static representation of the world.
Philosophical questions of life, love and lubrication are all dynamic, and Aristotle devoted significant effort to understand how things change and move through time. Aristotle’s curiosity led him to develop an early version of the scientific method, starting with a hypothesis and using experimentation to verify and/or modify the original idea. When thinking about motion, he observed that external effort was required to move a stationary object. Once the force was removed, experience showed him that the natural state of physical objects is that they move toward a state of rest. He found no exceptions and postulated that motion was merely a temporary reaction to a force. Thus, Aristotle divided the world into living beings and inanimate (not moving) objects.
Archimedes advanced the work of earlier philosophers and mathematicians to develop models to describe the workings of physical systems and mechanical devices. He may be described as the first true engineer because he applied knowledge to invent dynamic devices that are still useful today. Many familiar compressors and pumps are essentially modern versions of the Archimedes screw, and he also worked with levers, gears and pulleys. Archimedes’ work in these areas is well documented.
In 1901, the Antikythera mechanism
(see Figure 1) was found in a shipwreck off the coast of Greece. It was a bronze device which had moving wheels, gears and cranks that appear to calculate celestial motions. Archimedes is often identified as the inventor, and the mechanism even serves as the main plot device in an Indiana Jones movie (sorry, no more spoilers).
1
 Figure 1. A fragment of the Antikythera mechanism. Figure courtesy of Wikimedia Commons, CC BY-SA 3.0.
Figure 1. A fragment of the Antikythera mechanism. Figure courtesy of Wikimedia Commons, CC BY-SA 3.0.
We can only speculate whether the Antikythera mechanism was effective, but planetary motion has been studied for thousands of years. The paths of the sun and moon were predictable over long periods of time because they form a two-body orbital system with Earth;
2 solar timepieces including Stonehenge and sundials predated Pythagoras. But planets present a bigger challenge because (we now know) they do not orbit the Earth directly and follow elliptical (not circular) orbits. Geocentric models of the universe could only predict planetary positions over a few months, and needed constant corrections based on observational data. Today astronomers can predict planetary events years in advance with millisecond accuracy, but this ability required the rethinking of many assumptions about motion.
Recall Aristotle’s assertion that the natural state of earthly objects was at rest. Since we cannot feel the Earth moving, it is easy to conclude that it is not moving. But the sun, moon and planets move through the sky without slowing. Two different laws of motion were applied to account for these observations. Celestial objects were driven by divine forces and should move forever in perfect circular paths in the heavens. Meanwhile, the Earth was fixed, and inanimate objects must eventually come to rest on the surface. Living beings bridged the gap between the divine and the inanimate. They had the power to move in imperfect (non-circular) ways and would eventually die so their physical bodies would eventually return to Earth. And a great hero like Orion could achieve divinity and ascend to the heavens.
Even knowing the modern laws of physics, our brains default to the Aristotelian world view. When I was a college freshman, a classmate was returning from a fraternity party and had some trouble navigating the stairs. As everyone was laughing, his response challenged us to rethink the value of physics in the real world: “In class today, we learned that the Earth’s rotation at our latitude is represented by a vector tangential to the Eastern horizon with a magnitude 1,200 km/hour and an angle that changes by 15 degrees per hour. Meanwhile, the Earth revolves around the sun with a much higher magnitude of 30 km/second. After adding those vectors, we travel in a spiral pattern around the sun with the Earth moving by around 20 miles every time we take a step. Our physics professor took 15 minutes to calculate all that and gave an answer that was only accurate to a few significant digits. Even after a few beers, I can still do the mental math and missed the step by a few inches in 20 miles. What’s the big deal?”
In our everyday frame of reference, we ignore all of the rotation and revolution vectors because they cancel each other out. The heliocentric (sun-centered) solar system model makes the calculations easier for astronomers, but the rest of us have been successfully assuming a stationary Earth our whole lives.

Aristotle’s assertion matches everyone’s experience, and it was unchallenged for millennia until Galileo had a new idea. Aristotle’s assertion eventually became Aristotle’s fallacy.
Galileo
3 was convinced that the heliocentric model of the solar system was correct, but like our freshman, he was having trouble determining why we do not sense the motion of the Earth beneath our feet. He eventually developed the concept of inertia where moving bodies do not need an external force to remain in motion. Galileo’s inertia theory gave a different explanation: although the steps and the freshman are moving relative to the sun, they do not experience an external force related to the Earth’s motion because no external force exists, and none is required to maintain this straight line motion.
Inertia was a helpful concept, but until Newton and Leibniz independently invented calculus,
4 it was not possible to mathematically analyze systems that were undergoing incremental change and motion. With Newton’s Principia, which was published in 1687,
5 inertia was enshrined as the first of three laws of motion
(see Table 2). By including a universal force of gravity Newton could now explain why planets orbit in predictable, elliptical paths and also why we feel the weight of objects on Earth. Classical mechanics provided a set of rules that applied to everything whether on Earth or in the heavens. Although Einstein’s relativity modified some of the details, classical mechanics is still used to calculate most of the interactions necessary for tribology.
 Table 2. Laws of motion7
Table 2. Laws of motion7
Having finally developed an accurate mathematical framework to explain motion, one mystery remains: Aristotle’s fallacy. Newton’s first law of inertia directly invalidates Aristotle’s concept that motion is unnatural and objects eventually return to a state of rest. Our experience confirms Aristotle’s assertion, but all physicists agree that Newton’s laws are correct.
So, how could Aristotle possibly be wrong? Contemporaries called Aristotle “the man who knew everything” and he is remembered after more than 2,000 years. I consider myself lucky if my dog recognizes me after returning from an STLE annual meeting. But like all tribologists, I know about friction, which is the reason that Aristotle’s assertion became Aristotle’s fallacy.
REFERENCES
1.
“Indiana Jones and the Dial of Destiny” movie, 2023.
2.
From the geocentric perspective, both the sun and moon orbit the Earth.
3.
www.britannica.com/science/law-of-inertia
4.
Bardi, J. S. (2007),
The Calculus Wars: Newton, Leibniz, and the Greatest Mathematical Clash of All Time, Basic Books.
5.
Halliday, D., Resnick, R. and Walker, J. (2021),
Fundamentals of Physics, DeKalb, Ill.: J. Wiley & Sons, Inc.
6.
From
www.worldhistory.org
7.
http://en.wikipedia.org/wiki/Newton’s_laws_of_motion
8.
www.feynmanlectures.caltech.edu/I_15.html
9.
www.feynmanlectures.caltech.edu/I_17.html
10.
Smolin, L. (Feb. 1, 2006), “Atoms of space and time,” Scientific American. Available
here.
Tyler Housel is a technologist for Hnuco Technologies and is based in Lansdale, Pa. You can reach him at tylerhousel@comcast.net.