If you took your car apart, down to individual pieces, the largest pile of parts would undoubtedly be the threaded fasteners. This collection of nuts and bolts, screws and studs, carries the bulk of the load that holds your vehicle together. What keeps these fasteners in place, day after day, year after year, in good weather and bad? Friction!
Compared to other fastening methods (adhesive bonding, soldering, brazing, welding, etc.) threaded fasteners have the advantage of providing (relatively) easy disassembly and reassembly (i.e., serviceability). A simple example would be changing a flat tire. Imagine how difficult this task would be if the wheel was permanently mounted to the chassis!
The screw is one of the six classical simple machines, along with the lever, wedge, inclined plane, wheel and axle and pulley. From a mechanical analysis standpoint, however, there are only two. The pulley and the wheel and axle are circular levers, while the wedge and the screw are specific types of inclined planes. In particular, the screw is a spiral inclined plane.
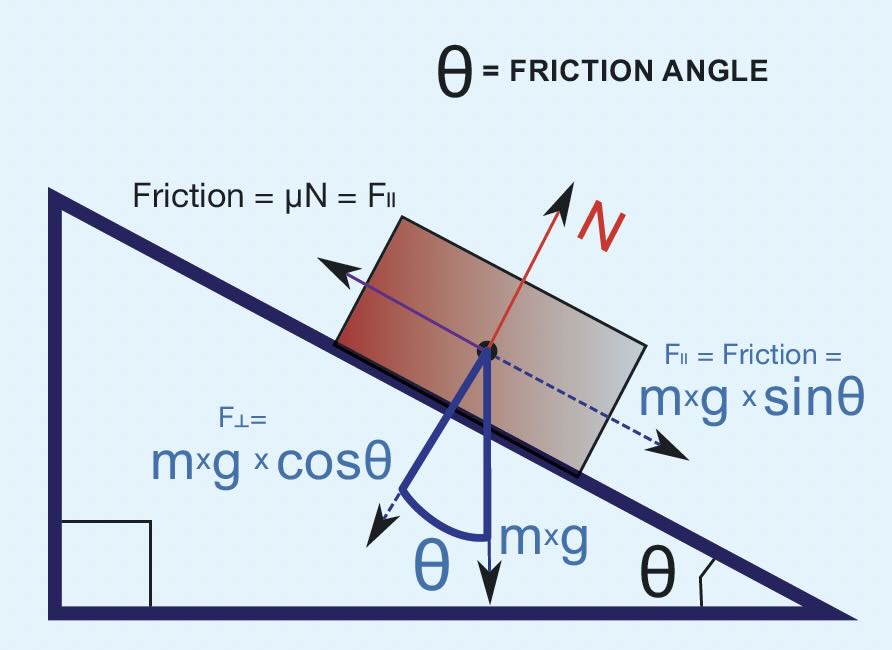Figure 1. Classical analysis of friction of an object on an inclined plane. Figure courtesy of derivative work: Wizard191 (talk)Option2_Freebodydiagram2_pn.png: Penubag, Public domain, via Wikimedia Commons.
Consider the classical analysis of friction of an object on an inclined plane, shown in Figure 1—where m is the mass of the object, g is the acceleration due to gravity, and N is the resultant force of the weight of the object perpendicular to the inclined plane. As the angle
q is increased, the coefficient of friction,
m, is simply tan
q when the object begins to slide (the “static” coefficient of friction) or when the object, if pushed down the ramp, continues to slide (the “dynamic” coefficient of friction). In either case, it is of considerable interest that the force balance during sliding gives the result:
m=tan(
q)
Observe that the value of
m is
independent of m, the mass of the object. If we add weight to the object, it will never begin to slide as long as the angle
q small enough that tan(
q) is less than
m. This condition is classically known as “self-locking.”
Consider a typical automotive bolt, where a typical value for the slope of the thread would be 3 degrees. In this case tan(3
°) is 0.052. Typical values of friction in automotive fasteners exceed 0.1, so no matter how large the axial force on a joint, the bolt will never spontaneously loosen.
There are many uses for screws besides fastening. Screws are widely used to convert rotary motion into liner motion, including many small motors such as the power seat adjusters that are likely present in your vehicle. In fact, nearly every screw-based machine converts rotational motion into linear motion, except one. The “Yankee drill” or “Yankee screwdriver” is the only machine (that I know of) that converts liner motion into rotation. If you haven’t seen this device in action, check out the movie “The Blues Brothers.” Elwood Blues (played by Dan Aykroyd) uses this device to quickly remove the control panel and disable the elevator near the end of the movie.
Ed Becker is a Fellow and Past President of STLE. He is currently president of Friction & Wear Solutions, LLC and can be reached through his website at www.frictionandwearsolutions.com.