Meet the Presenter
This article is based on a webinar presented by Jim Woodhouse and Auburn University on Oct. 5, 2021, titled Violin Strings and the Tribology of Rosin. The webinar series, titled The Beard Tribology Webinar Series, is named after the late Ralph Beard, who pioneered the study of tribology at Auburn. For more information on the webinar series, visit www.eng.auburn.edu/programs/tribology/beard-tribology-webinar.html.

Jim Woodhouse took a first degree in mathematics at Cambridge University followed by a doctorate on the acoustics of the violin in the Department of Applied Mathematics and Theoretical Physics at Cambridge University. He worked for the engineering consultancy firm Topexpress on a variety of structural vibration problems, prior to joining the Department of Engineering at Cambridge University in 1985. Woodhouse is an expert on the design and fabrication of instruments and how that influences their acoustics. He is experienced not only in the physics behind instruments but in the details of fabricating them. His research interests involve vibration, with musical instruments forming a major part of his research. Currently retired, his research interests include:
• mechanics of musical instruments (https://euphonics.org/),
• brake squeal and other frictionally excited vibration,
• vibration of complex structures and
• identification and modeling of vibration damping.

You can reach Woodhouse atjw12@cam.ac.uk.


Jim Woodhouse 

---

KEY CONCEPTS
• Rosin, a natural resinous material used to coat the hairs of bows on musical instruments, mediates the friction applied to the string of the instrument. Predicting the frictional force put on the strings of an instrument by the bow may be one of the hardest tribology problems.
• Historically, scientists assumed the Stribeck friction model worked in these situations, but the model does not capture the details of transients, which matters to musicians who care how it sounds and feels to the hand on the bow.
• A layered thermal model may be more accurate in accounting for the shear band that forms within the rosin as it heats; however, the waveforms still look wrong.

The bowing of a violin string is a deliberate stick-slip vibration, notes Jim Woodhouse, professor emeritus of Cambridge University in England, UK. The friction against the string is mediated by rosin, a natural resinous material musicians use to coat the hairs of the bow. The hardest tribology problem is related to accurate prediction of the frictional force put on the strings by the bow. Violinists care about the details—how it sounds and how it feels under the hand on the bow.

This article is based on a webinar presented by Woodhouse and Auburn University. See Meet the Presenter for more information.

A question Woodhouse seeks to answer is: can the physics be understood well enough for computer simulations of this vibration to be useful to violinists? The answer is maybe, as scientists are still struggling to develop a model that works well.

Violin string vibration
In the 1870s, German scientist Hermann von Helmholtz worked out what happens when a bow moves across a string, and the resulting motion of a bowed string is called Helmholtz motion (see Figure 1). At any moment, the string is in a triangular shape with a sharp corner that travels back and forth. The string alternately sticks and slips across the bow at the natural vibration period of the string, the timing being determined by when the “Helmholtz corner” passes the string. The string motion is measured using a sensor embedded in the bridge of the violin.


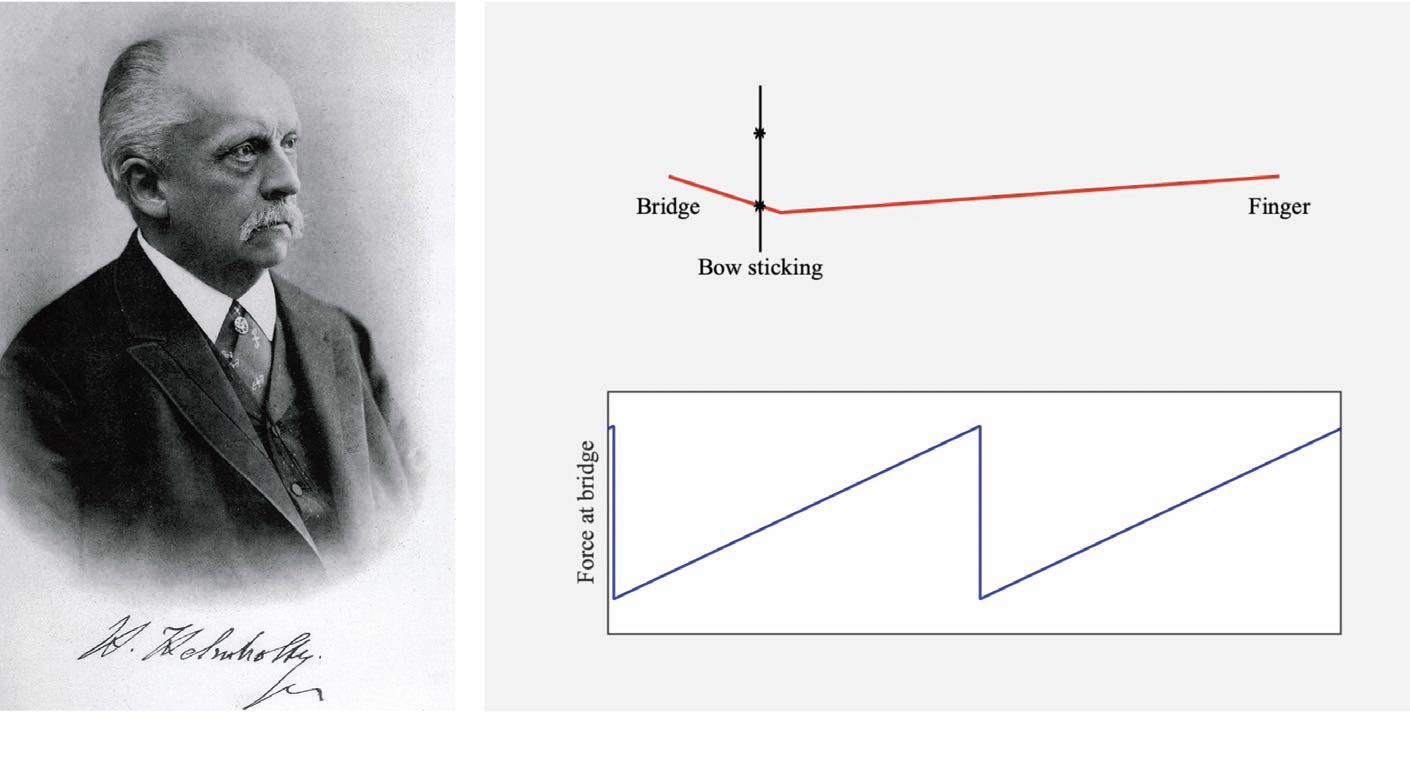Figure 1. German scientist Hermann von Helmholtz worked out what happens when a bow moves across a string, and the resulting motion of a bowed string is called Helmholtz motion. Image of Hermann von Helmholtz courtesy of Meisenbach, Riffarth & Co. Berlin. Scanned, image processed and uploaded by Kuebi = Armin Kübelbeck, Public domain, via Wikimedia Commons.

As well as Helmholtz motion, a violin string can vibrate in many different ways, mostly bad (e.g., double-slipping motion, multiple flyback motion, raucous motion). Woodhouse investigated these using systematic experiments with a computer-controlled bowing machine (see Figure 2) that used a Perspex rod coated in rosin. Particularly important to the sound quality are the transient motions of bowed strings, how a note starts and how a note ends. Subtle differences in transients make a big difference to a musician, and Woodhouse asks, are there any other tribology applications where such small details matter?


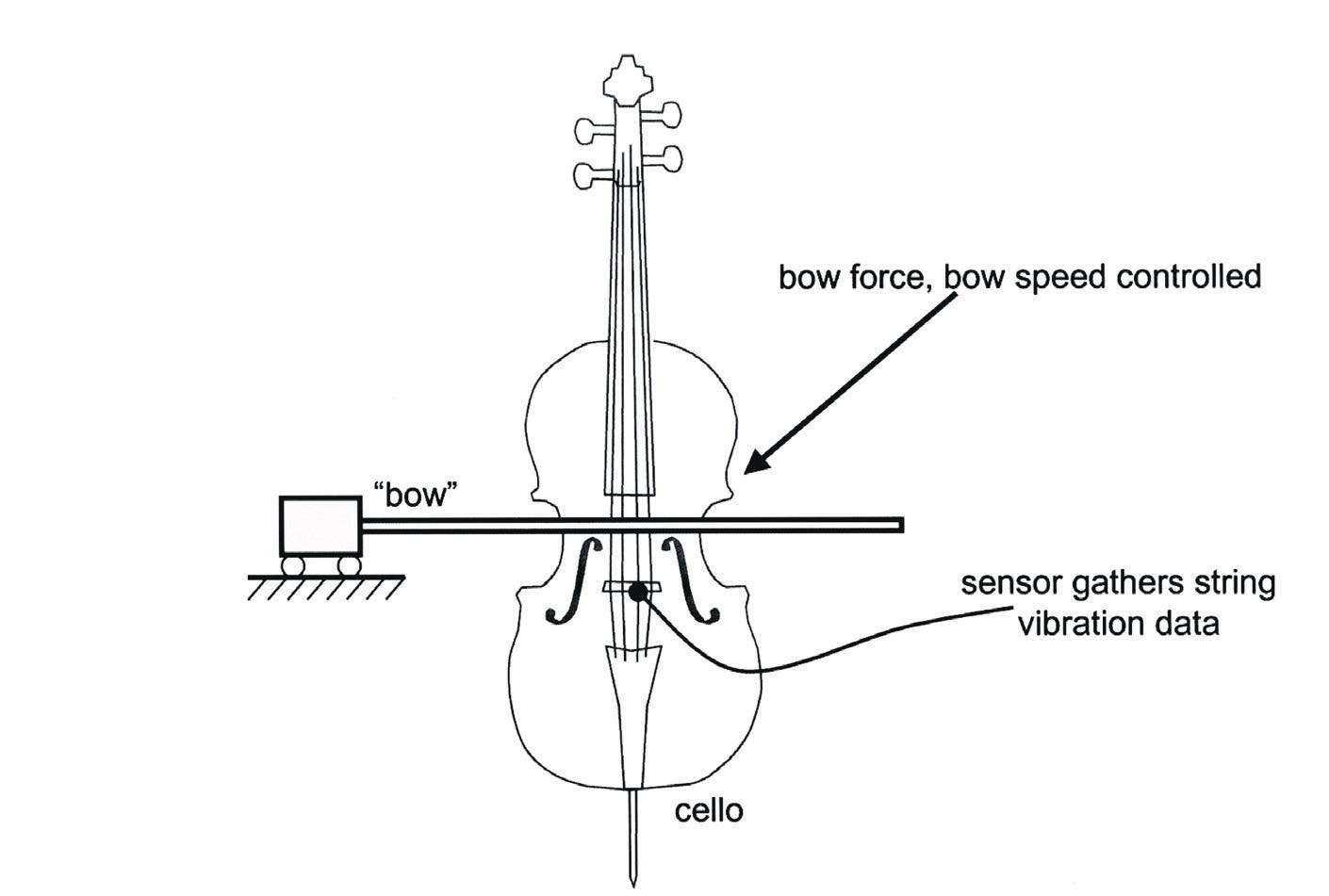Figure 2. Systematic experiments with a computer-controlled bowing machine that used a Perspex rod coated in rosin.

Do theoretical models perform well enough to simulate transients reliably? The violin string and the body of the instrument are complicated linear systems that are quite well understood, but the friction force between the bow and the string is governed by a nonlinear friction law.

Until perhaps 20 years ago, the Stribeck curve model of friction was thought to control the results. Figure 3 shows the coefficient of friction of violin rosin plotted against the sliding speed to give the steady friction force Stribeck curve. The assumption was that during transient vibration, the friction force simply tracked along this curve, according to the instantaneous sliding speed. Woodhouse observes that many scientists think this is all there is to know about sliding friction.


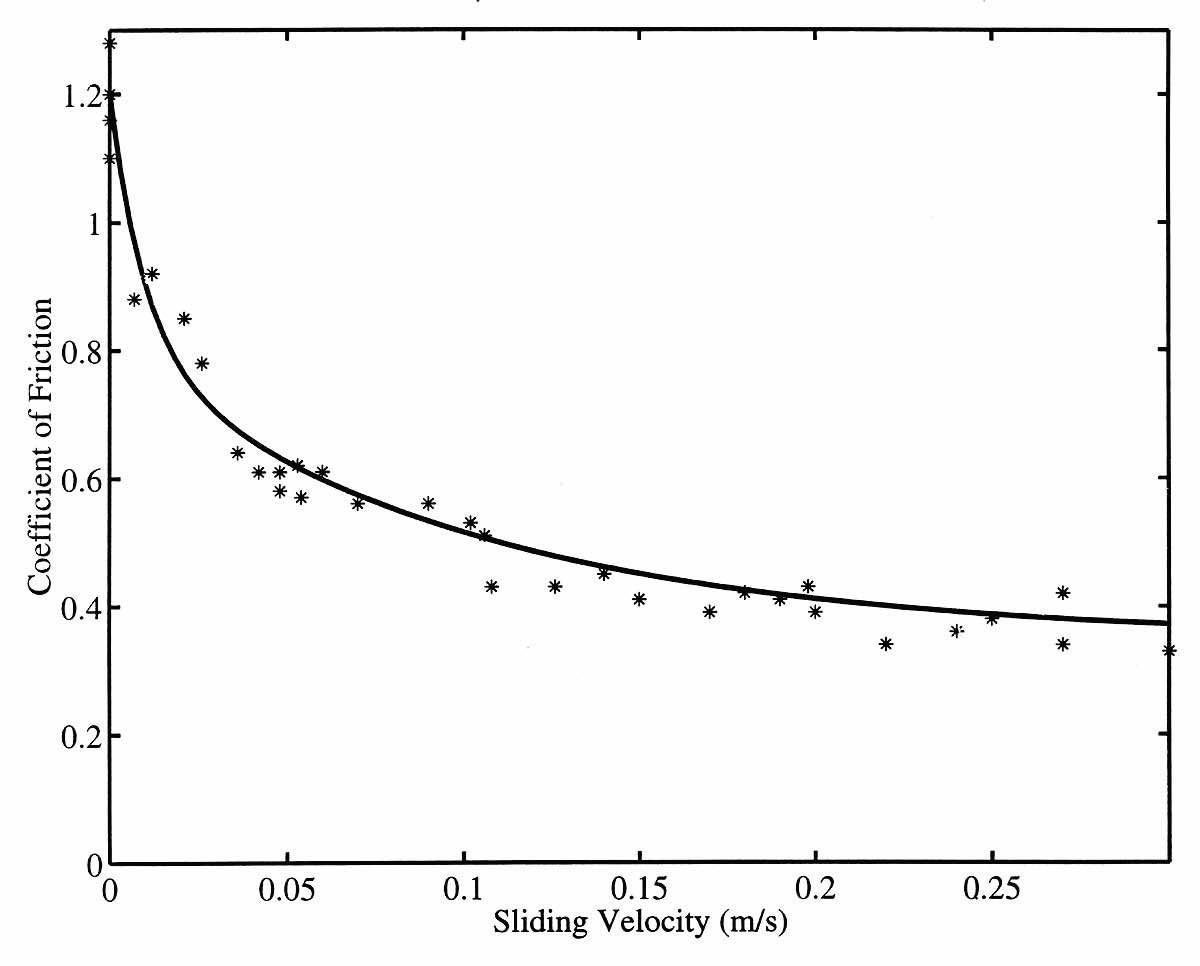Figure 3. The coefficient of friction of violin rosin plotted against the sliding speed to give the steady friction force Stribeck curve.

This modeling approach shows some early successes with qualitatively good simulations of Helmholtz motion and other periodic regimes. This approach also is qualitatively correct for variation with bow force and bowing position; however, this method did not do well at modeling transients.

Why do we want computer models of a bowed string? How the instrument feels under the hand of the player is important. Players make judgments of the sound and ease of playing an instrument. Woodhouse asks, what do those judgments mean in relation to the scientific models?

To answer these questions, Woodhouse looks at transients. A simulation model can be used to investigate questions of “playability”—that is, does a given bow gesture produce Helmholtz motion? How long does the initial transient take? Does a similar bow gesture produce a similar transient, or is this system twitchy? How are the answers to these questions influenced by:
• properties of the string,
• properties of the violin body,
• properties of the bow or
• properties of the rosin?

The goal is to explore these sensitivities in the computer. The Guettler diagram (see Figure 4) is a two-dimensional family of bow gestures with bow force on the y-axis and bow acceleration on the x-axis. This results in a diagram that shows where it might be possible to perform a “perfect” transient. The experimental results tested a bow on the string with a given fixed bow force and bowing using a chosen constant acceleration. However, simulation results with the Stribeck model did not match the experimental results, so something must be wrong with the simulation.


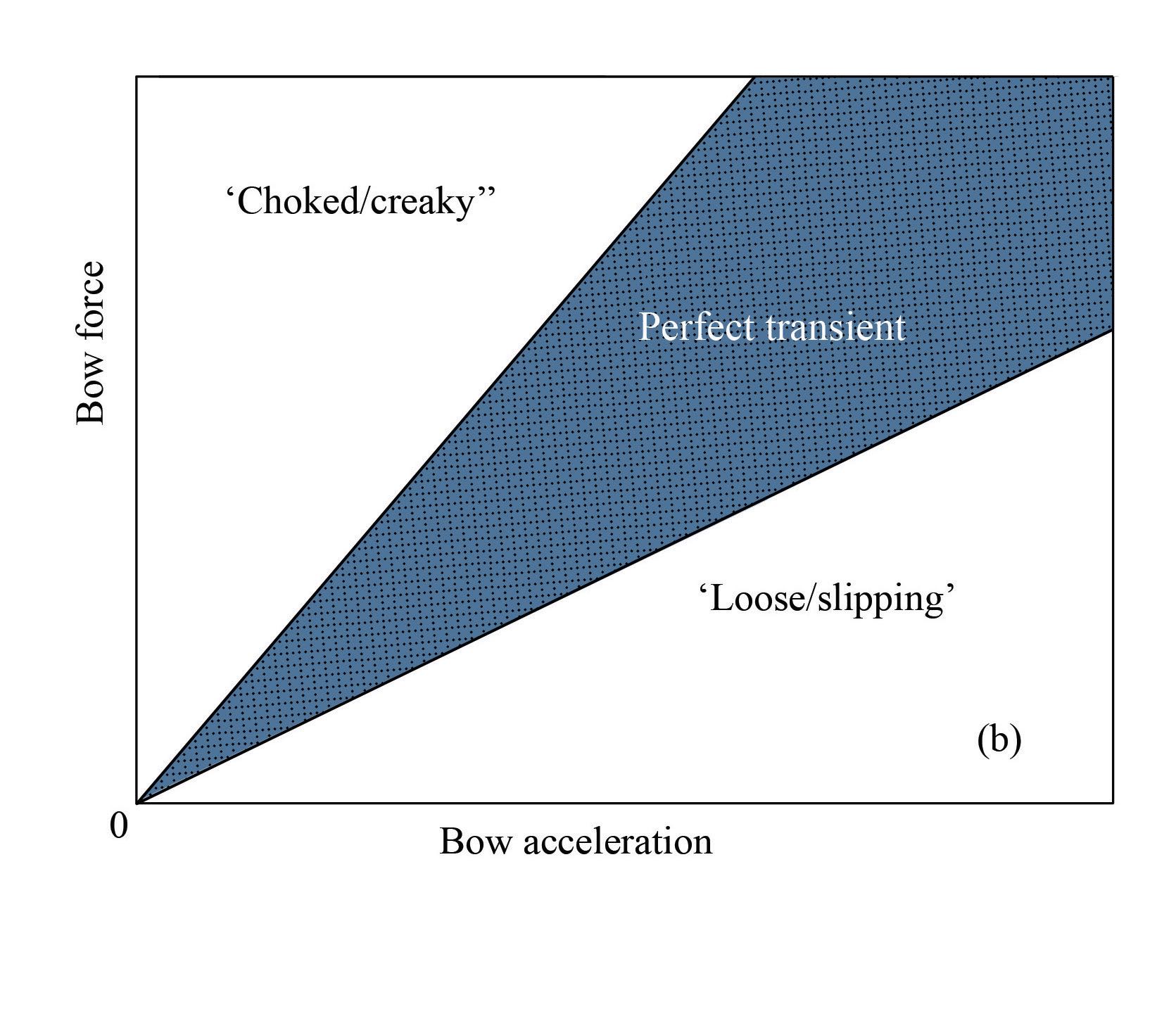
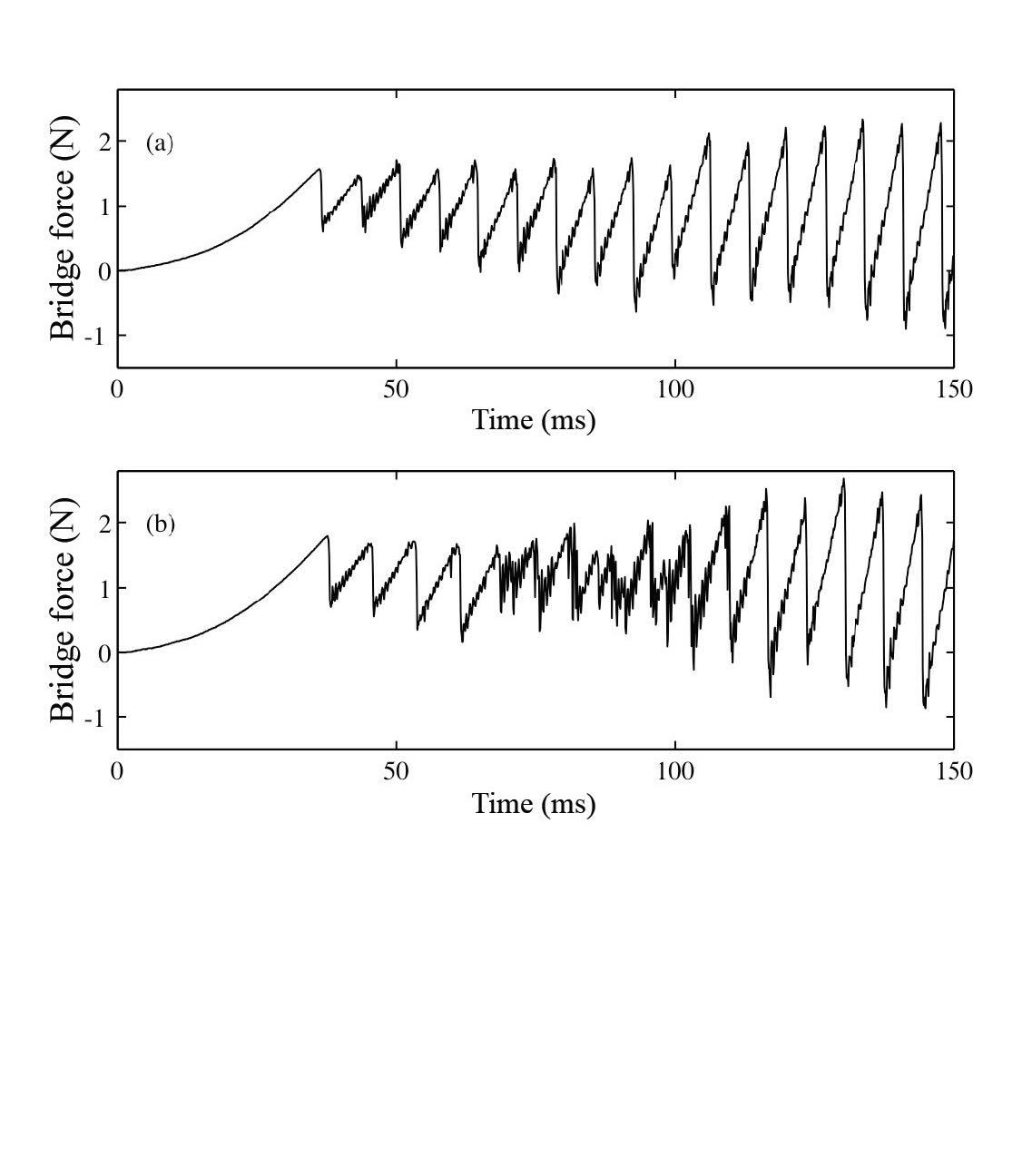Figure 4. The Guettler diagram is a two-dimensional family of bow gestures with bow force on the y-axis and bow acceleration on the x-axis.

Thermal model
In response to this conclusion, a thermal model was tried. The friction of rosin is influenced by temperature at the contact. Rosin is a glassy material, with a glass transition temperature near room temperature—its mechanical properties vary rapidly with temperature. In a crude model, the computer used averaged temperature in the contact region and let yield strength of the rosin depend on this temperature. Rosin in the contact region is heated by frictional work and cooled by conduction and convection. A heat-flow calculation in parallel with dynamic simulation gives the temperature history. Yield stress varies by temperature.

Figure 5 shows the comparison of measured and simulated Guettler diagrams. Figure 6 shows some waveforms of actual measured results versus the Stribeck friction model results and the thermal friction model results. These thermal results are better but still not good enough.


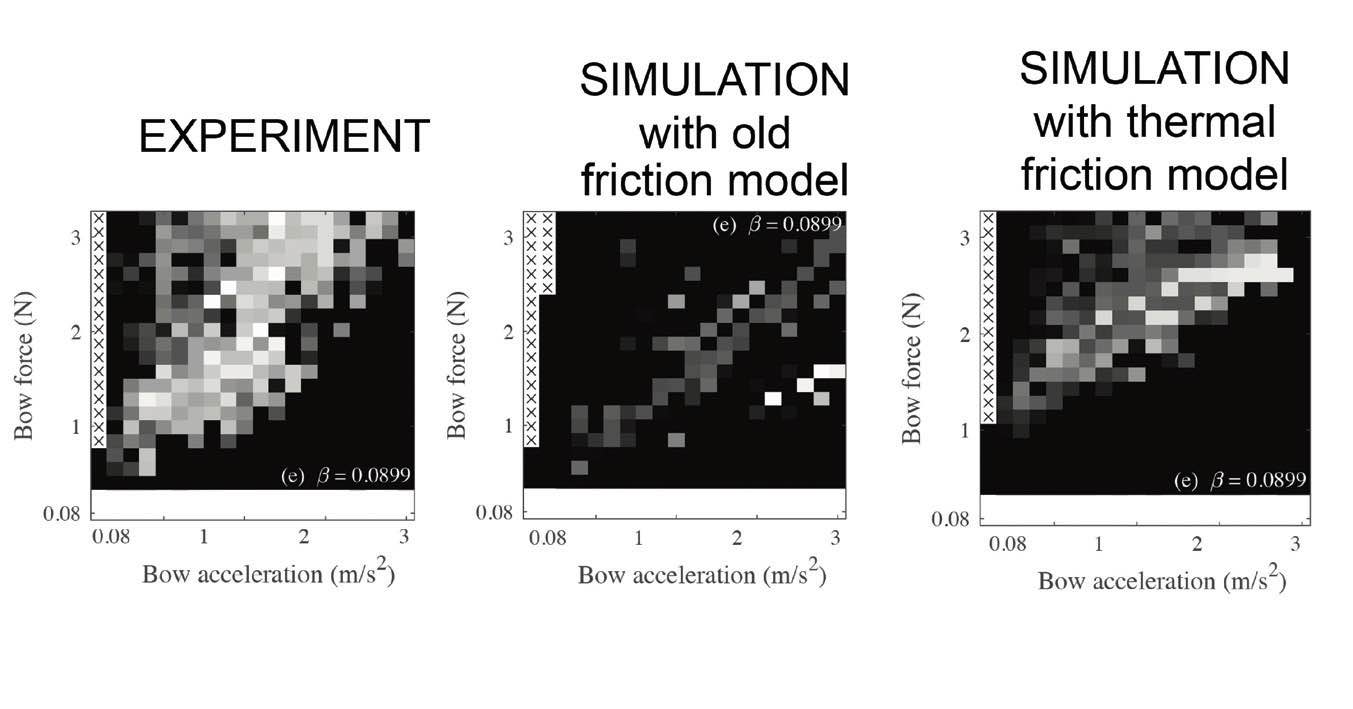Figure 5. The comparison of measured and simulated Guettler diagrams.


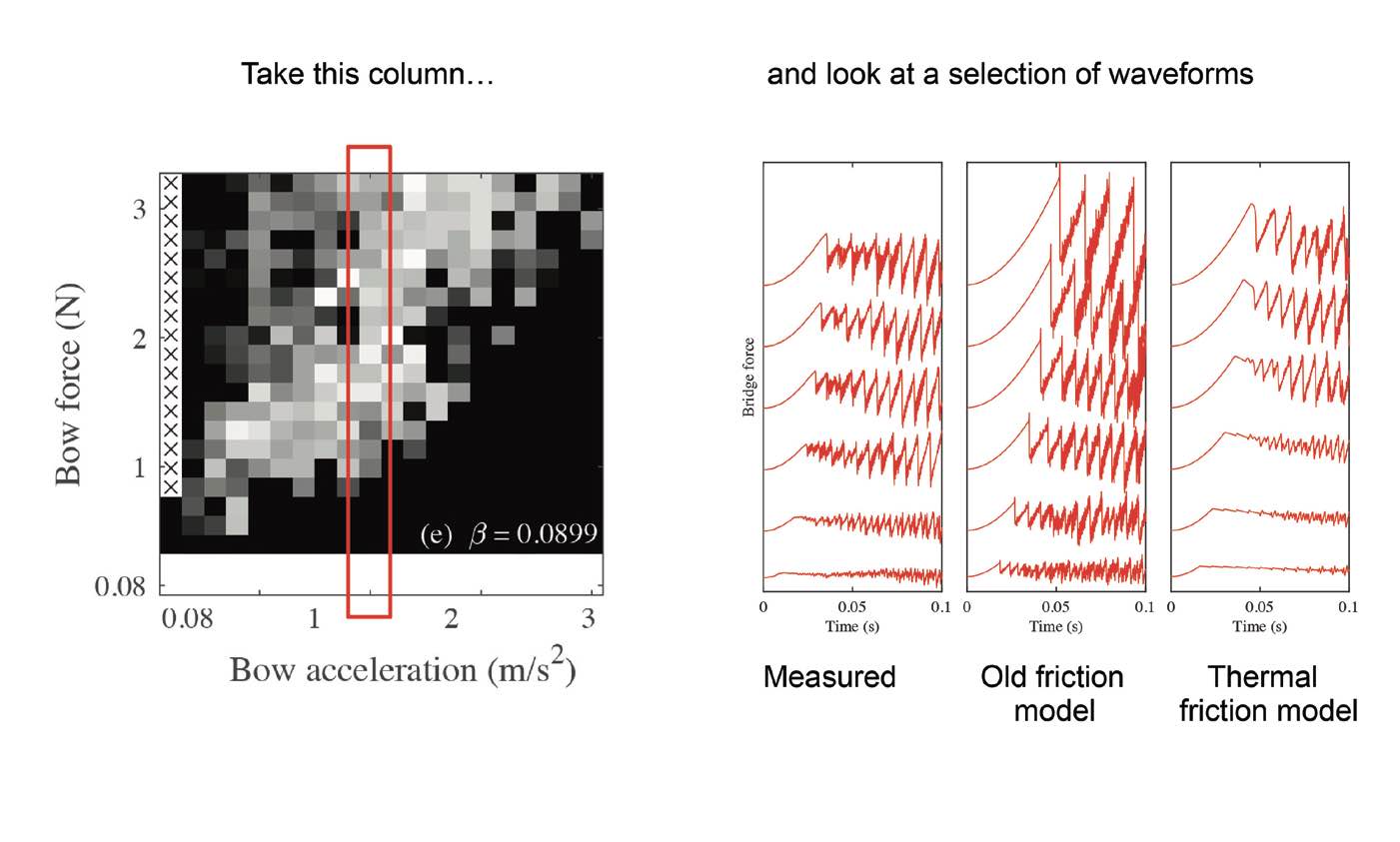
Figure 6. Some waveforms of actual measured results versus the Stribeck friction model results and the thermal friction model results.

Glass bow rig
Different evidence came from a bowed-string test rig at Carnegie Mellon University operated by Bob Schumacher. The “bow” in this case was a rosin-coated glass rod. By measuring the forces at the string’s terminations, the force and velocity at the contact point can be inferred by inverse calculation. Figure 7 shows data from the “glass bow” rig at Carnegie Mellon University, while Figure 8 shows scanning electron micrographs of the wear tracks on the rosin surface. These wear tracks show the rosin melting during rapid slipping but behaving more like a solid during sticking intervals. Woodhouse notes, as a side comment, this behavior is a “mirror image” of lubricated rolling with temperature and pressure.


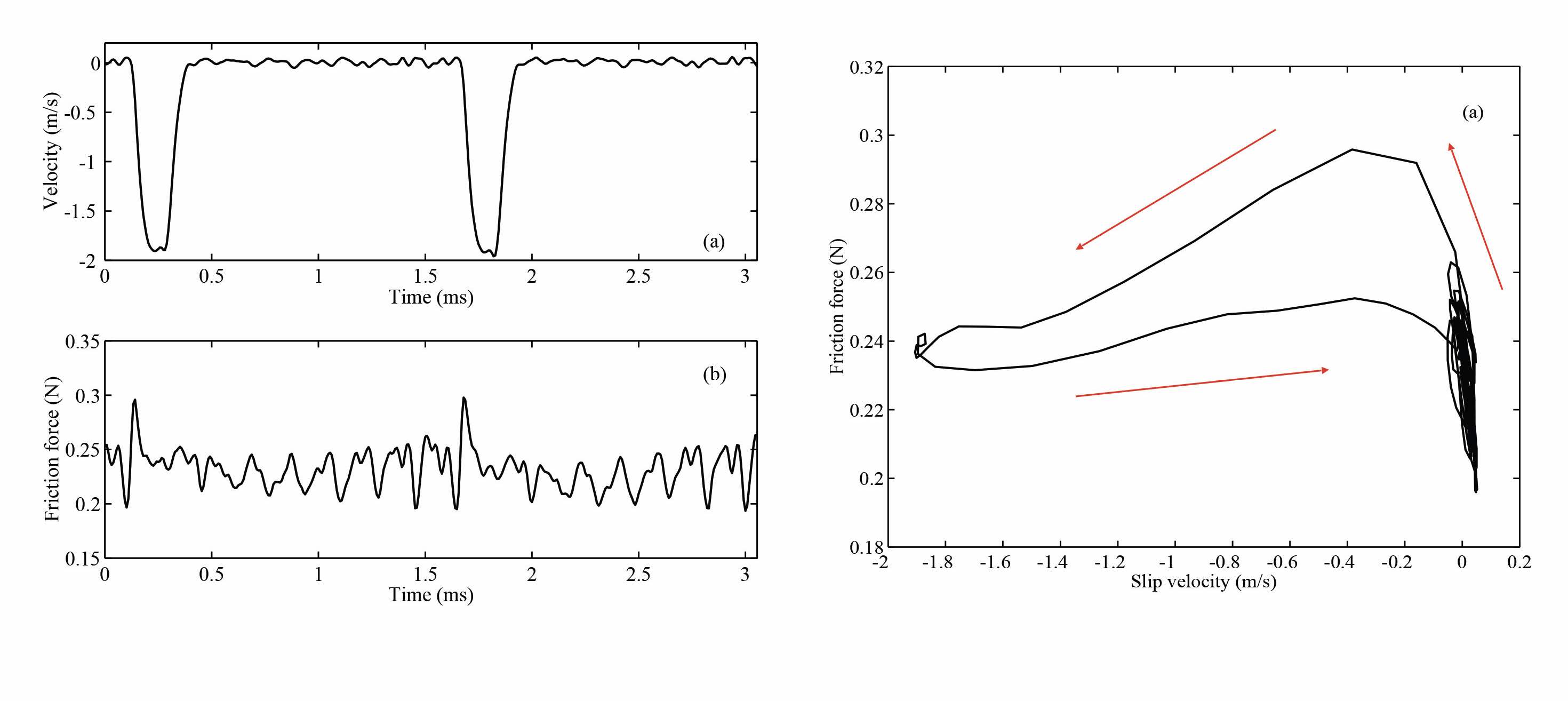Figure 7. Data from the “glass bow” rig at Carnegie Mellon University.


Figure 8. Scanning electron micrographs of the wear tracks on the rosin surface.

Rosin
Woodhouse next asks if friction can be modeled in terms of the bulk properties of rosin. He looks at measurements using a differential scanning calorimeter and rheometry to answer this question.

The Eyring model (see Figure 9) is a possibility for a best guess for a constitutive law. Adding elasticity to this formula (see Figure 10) results in a plausible model to try. Figure 11 shows the complex shear modulus versus temperature for violin rosin. The gap in the middle of the curves is caused by having to use different testing machines when rosin is a solid versus when it is a liquid. This shows that parts of the data fit the Eyring model but not all of it.


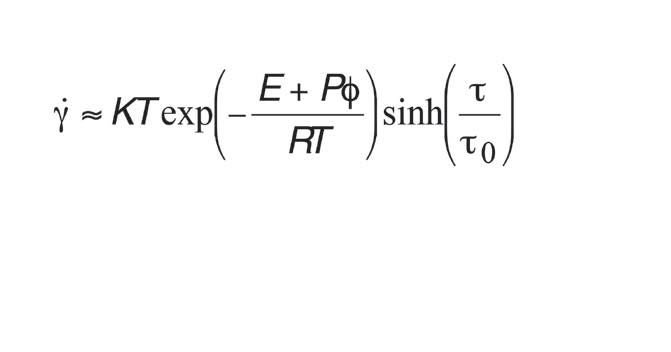Figure 9. The Eyring model is a possibility for a best guess for a constitutive law.


Figure 10. Adding elasticity to this formula results in a plausible model to try.


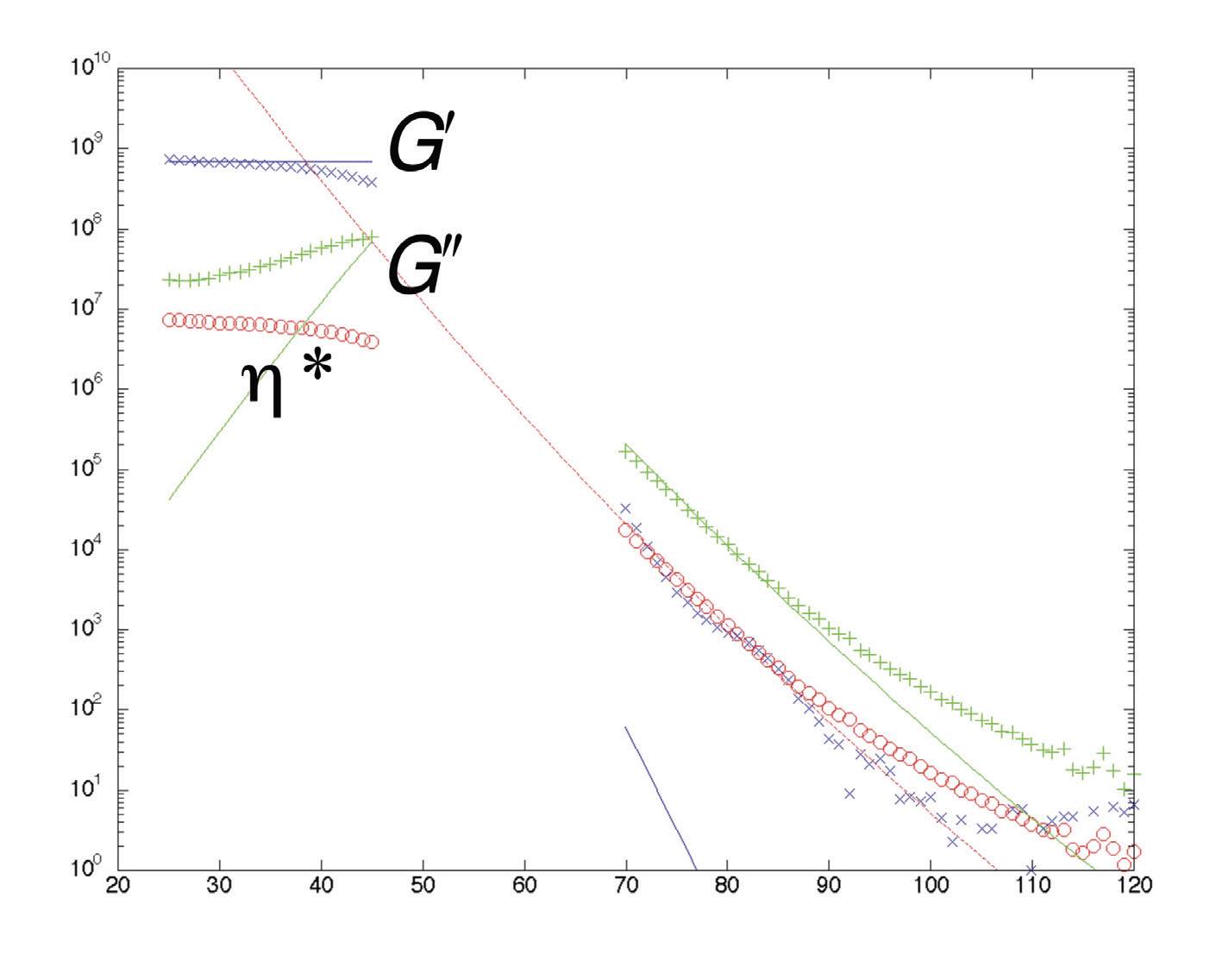
Figure 11. The complex shear modulus versus temperature for violin rosin.

Enhanced heat-flow model
This Eyring model was applied to an enhanced heat-flow simulation allowing the rosin layer to have different temperatures at different depths. Woodhouse notes that everything is speculative from here on as there is still unfinished business in understanding this model. When Helmholtz motion is imposed on the graph (see Figure 12) during the slipping phases, the mean temperature increases. This model predicts shear band formation within the rosin. The slip is concentrated in a thin 200-nanometer-thick band near the middle of the rosin layer.


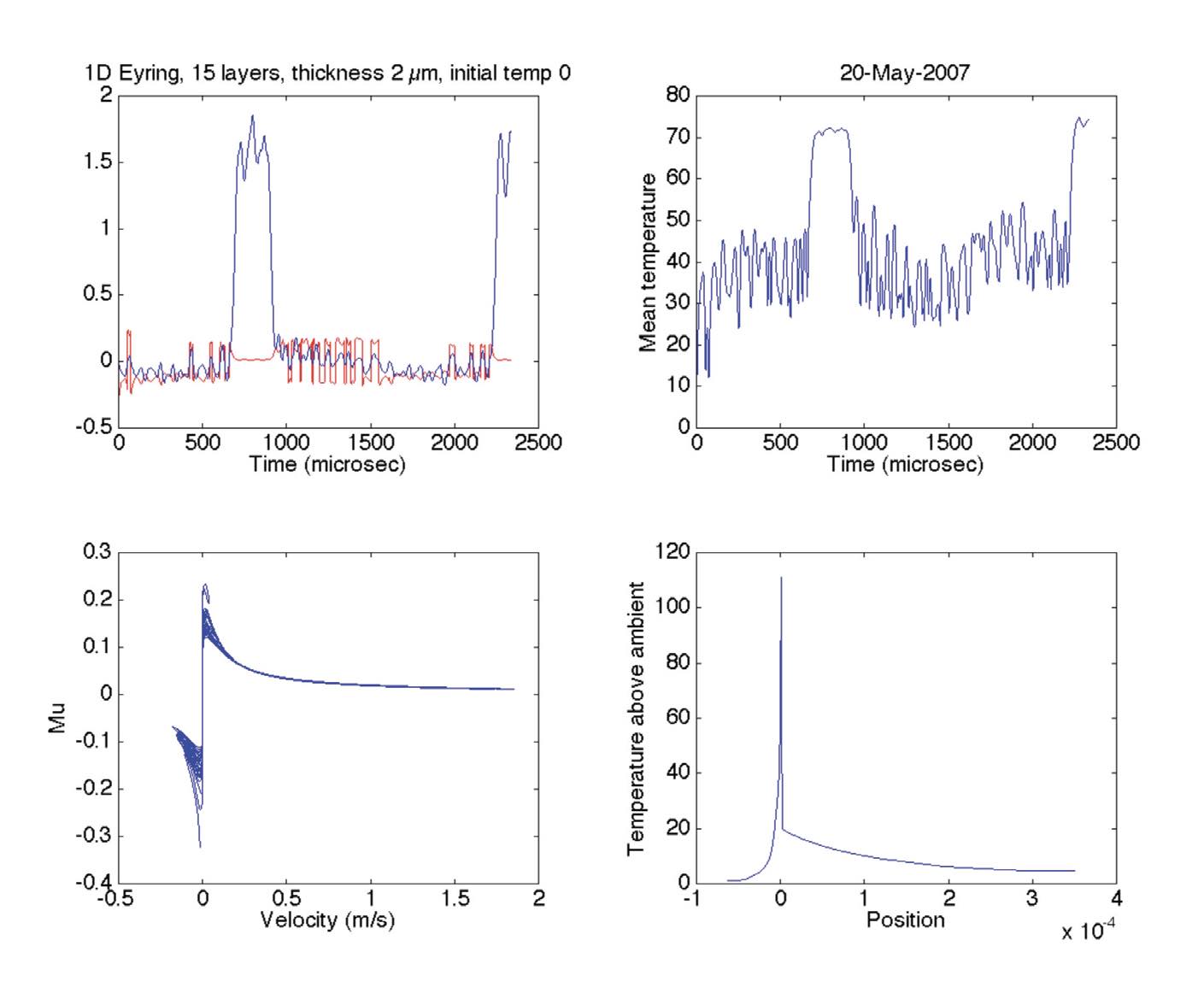Figure 12. Impose measured Helmholtz motion.

Summary and puzzles
Woodhouse presents the following conclusions:
• Models of a bowed string can give a qualitative match to different vibration regimes. However, to be relevant to musicians, these models must be good enough to capture details of transients, which the Stribeck friction model gets badly wrong.
• A model based on the thermal properties of rosin can do better. This thermal behavior seems to be the reason rosin is used in the first place.
• A layered thermal model can produce “stick-slip” behavior without an explicit switch of states by spontaneously creating a shear band within the rosin layer where it got hot.
• The snag in the layered thermal model is that the waveforms look wrong. The apparent coefficient of friction at the end of the slip is an order of magnitude smaller than what is observed.
• Woodhouse quotes David Tabor, who wrote, “There is some evidence that the phase change is relatively sluggish. Thus [this Eyring model] must be applied with some caution since the lubricant film is in the contact region for a very short time.”¹

Slideways or problems where friction excites vibration are examples of tribology problems that might be similar to violin strings. Brake squeal in vehicles is an example; however, in brake squeal problems, the researchers don’t care about transients. They only care about whether it squeals.

Woodhouse notes that rosin may need to be studied at the molecular level to solve these questions.

REFERENCE
1. Tabor, D. (Nov. 29, 1991), Gases, Liquids and Solids and Other States of Matter, 3rd edition, Cambridge University Press.

Andrea R. Aikin is a freelance science writer and editor based in the Denver area. You can contact her at pivoaiki@sprynet.com.