Extra-extra-extrapolation
Evan Zabawski | TLT From the Editor June 2021
How far is too far?
Life extension tables are problematic. On one hand, they offer an easy-to-use format for determining how much a change in particle count or moisture level can have on the relative life of in-service oil. But, on the other hand, they might be perpetuating a false sense of purpose.
Take a life extension table for moisture levels as an example. A recent article published a version with data that followed a fairly evident pattern; it suggested that reducing water concentration from 50,000 ppm to only 2,500 ppm would extend the mean time between failures by a factor of 6, but that the factor was unchanged if the reduction was from 5,000 ppm to 250 ppm, or even 500 ppm to 25 ppm.
What this table seems to suggest is that an identical (99.5%) reduction in water concentration will extend the life of a machine by the same amount, regardless of the initial moisture content—a tidy, direct relationship without qualification on machine or oil type to prevent applying this information indiscriminately.
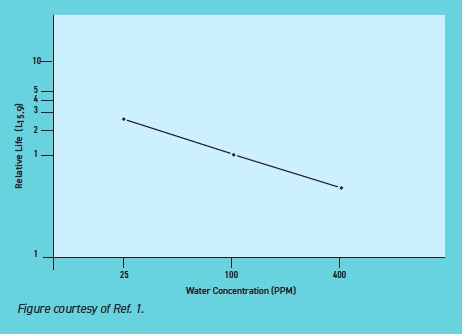
The results of a study on the effect of water on bearing life that were presented at the American Society of Lubrication Engineers (ASLE, now STLE) Annual Meeting in 19761 provides some valuable insight. The study was conducted to determine bearing fatigue life using tapered roller bearings lubricated with an SAE 20 oil with water concentrations of 25, 100 and 400 ppm. The results are pictured, normalized to a relative life of 1 for 100 ppm water concentration, and the slope of the line was determined. From the slope, a relative life equation was derived as L = (100/X)
0.6, where L is relative life and X is water concentration. Therefore, each 75% reduction in water content (from 400 ppm to 100 ppm, or from 100 ppm to 25 ppm) results in the same 2.3X life extension.
The water concentrations were chosen because they “can be encountered in many applications due to changes in the relative humidity,” but the question is, just how high of a water concentration can the data be extrapolated reliably? Should we believe the equation when it estimates the same 2.3X life extension when reducing water concentration from 1,600 ppm to 400 ppm, or how about 6,400 ppm to 1,600 ppm?
At some level, the water concentration will reach a point where its state will change from dissolved to emulsified or free, and its effect will be so detrimental that any further increase is likely to be inconsequential. As an example, the life of a bearing lubricated with 25% water versus 100% water would be extraordinarily short in both cases, but oddly enough, if a bearing lubricated with 100% water reached its fatigue life in only one minute and a bearing lubricated with 25% water reached its fatigue life in 2.3 minutes, the equation is not wrong. The practicality, however, is that the extra 1.3 minutes of bearing life is trivial.
Furthermore, the bearings in this study were subjected to a “2.03 GPa maximum compressive stress at 2,700 rpm and the operating temperature was maintained at 150 F (66 C),” but bearing life has a strongly inverse relationship with both speed and load, so the equation should not be trusted at other speeds or loads.
Using the equation on the first example of 50,000 ppm and 2,500 ppm, the results are that 50,000 ppm has a relative life of ~2.4% and 2,500 ppm has a relative life of ~14.5%, making the life extension factor for a 75% reduction in water concentration ~6.03X—a remarkable coincidence!
So, can we trust data obtained between 25 and 400 ppm as a valid indicator for behavior between 2,500 and 50,000 ppm, even if such short bearing lives were meaningful? Can we trust it at other speeds and loads, or even on other machine parts, or using different oil? Not really.
The axiom is that we must keep lubricants cool, clean and dry, and we shouldn’t need a table to realize that 50,000 ppm, or even 5,000 ppm, is not dry enough for optimal lubrication in most applications.
REFERENCE
1.
Cantley, R.E. (1977), “The effect of water in lubricating oil on bearing fatigue life,”
ASLE Transactions, 20 (3), pp. 244-248, DOI: 10.1080/05698197708982838.
Evan Zabawski, CLS, is the senior technical advisor for TestOil in Calgary, Alberta, Canada. You can reach him at ezabawski@testoil.com.