RESULTS AND DISCUSSION: Fig. 2 presents the static friction coefficient m as a function of t/R when Eco/Esu = 4, Eco/Yco = Esu/Ysu = 1000 under the dimensionless normal load P* = 50, where E and Y indicate Young’s modulus and yield strength, respectively, and subscripts ‘co’ and ‘su’ indicate coating and substrate material, respectively. P* is defined as P/(EsuR2×10-7). Since Esu and R are fixed, the dimensional normal load P is proportional to P*. Thus, results in Fig. 2 are in fact obtained under the same dimensional normal load P. As a result, only the effect of the geometry parameter t/R on the static friction coefficient is revealed in Fig. 2. The static friction coefficient m first increases linearly with t/R from msu at t/R = 0 till reaching a maximum mm at (t/R)m. Further increase of t/R above (t/R)m leads to a decreasing m that eventually approaches mco.
In a homogeneous spherical contact [4], a more plastic and compliant junction results in a lower m and a junction of larger size can support a larger friction force. It was also found that a thicker hard coating better protects the substrate from plastic deformation and results in a smaller contact area at the coating outer surface [5]. Hence, for t/R from 0 to (t/R)m, where the substrate is the dominant component of the coated system, increasing t/R will reduce the plasticity level in the substrate and therefore increase m. On the other hand for t/R above (t/R)m where the coating is the dominant component increasing t/R will reduce the contact area thereby reducing m.
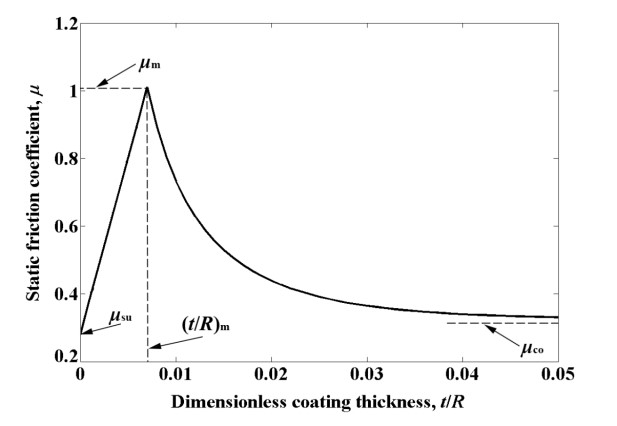
Figure 2 The static friction coefficient m as a function of t/R for Eco/Esu = 4, Eco/Yco = Esu/Ysu =1000 and P* = 50.
REFERENCES: 1. Holmberg, Surf. Coat. Tech. (2007), 2. Greenwood, T. Roy. Soc. (1966), 3. Keer, Int. J. Solids. Struct. (1991), 4. Brizmer, Tribo. Let.t (2007), 5. Chen, Tribo. Int. (2017).